Unit Circle Chart: A Comprehensive Guide
Introduction
The unit circle is a fundamental concept in trigonometry, serving as a bridge between geometry and algebra. By understanding the unit circle chart, students and enthusiasts can gain deeper insights into trigonometric functions and their applications.
Understanding the Unit Circle

A unit circle is defined as a circle with a radius of one unit, centered at the origin (0,0) of the Cartesian coordinate system. This simple definition lays the groundwork for exploring the relationships between angles and trigonometric functions.
Historical Background
The concept of the unit circle has its roots in ancient civilizations. Babylonian and Egyptian mathematicians used early forms of trigonometry for astronomical calculations. The formalization of the unit circle, however, is credited to Greek mathematicians like Hipparchus and Ptolemy, who developed trigonometric tables and concepts that closely resemble the modern unit circle.
Mathematical Foundations
Equation of the Unit Circle
The standard equation of a circle is:
(x – h)² + (y – k)² = r²
For a unit circle centered at the origin, this simplifies to:
x² + y² = 1
This equation is pivotal in deriving the sine and cosine values for various angles.
Trigonometric Functions
On the unit circle:
- cos(θ) corresponds to the x-coordinate.
- sin(θ) corresponds to the y-coordinate.
This relationship allows for the definition of all six trigonometric functions based on the coordinates of points on the circle.
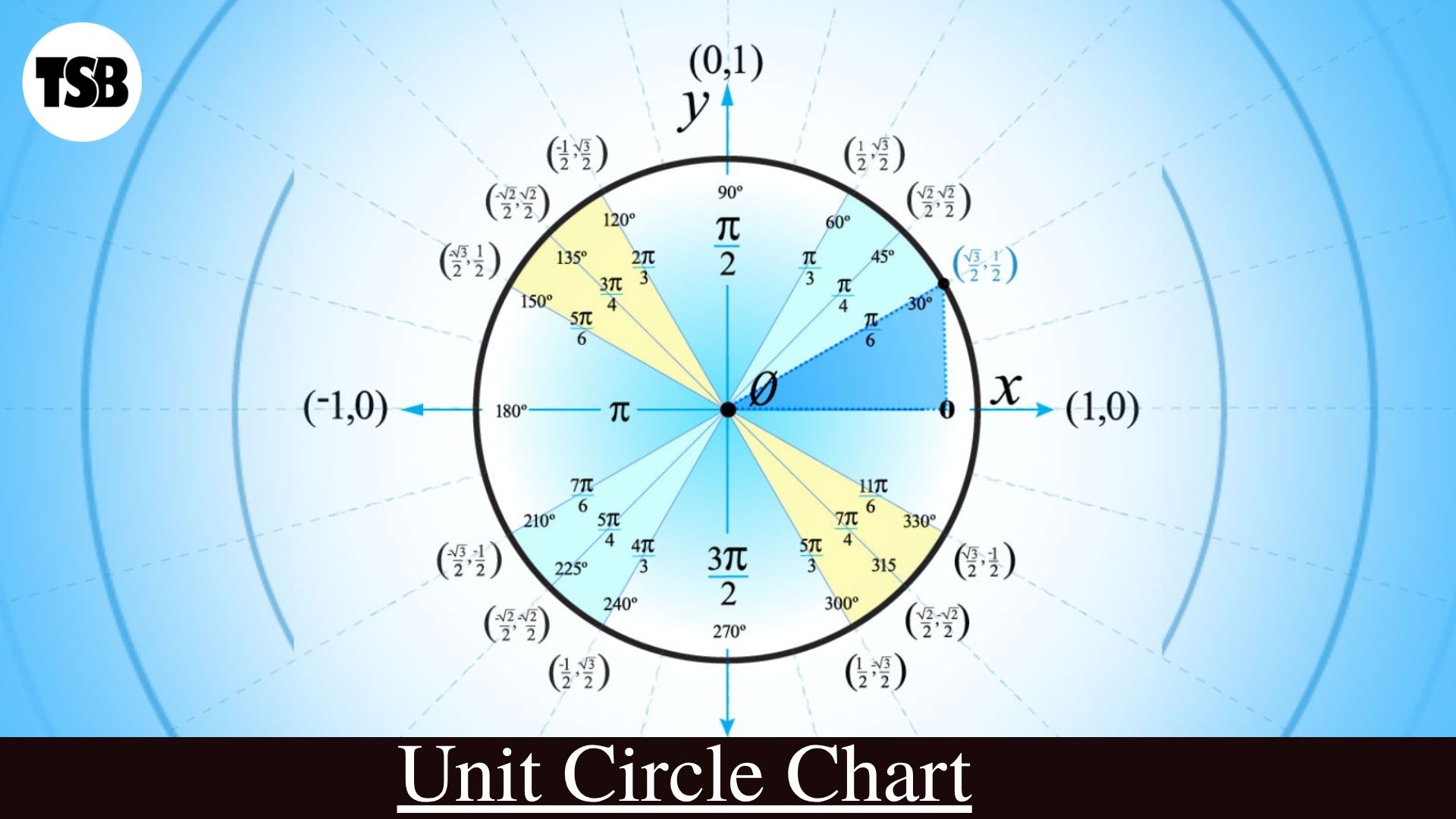
Constructing the Unit Circle Chart
Creating a unit circle chart involves plotting angles in both degrees and radians, and identifying their corresponding sine and cosine values.
Key Angles and Coordinates
| Degrees | Radians | Coordinates (cos(θ), sin(θ)) |
|---|---|---|
| 0° | 0 | (1, 0) |
| 30° | π/6 | (√3/2, 1/2) |
| 45° | π/4 | (√2/2, √2/2) |
| 60° | π/3 | (1/2, √3/2) |
| 90° | π/2 | (0, 1) |
These values repeat in each quadrant, with appropriate sign changes based on the quadrant’s characteristics.
Applications in Trigonometry
Solving Trigonometric Equations
The unit circle aids in solving equations like sin(θ) = 1/2 by identifying all angles θ where the sine value is 1/2.
Graphing Trigonometric Functions
Understanding the unit circle allows for accurate graphing of sine, cosine, and tangent functions, highlighting their periodic nature and amplitude.
Real-World Applications
Trigonometry and the unit circle are used in various fields, including:
- Engineering: for analyzing wave patterns.
- Physics: in studying oscillatory motions.
- Computer Graphics: for rotations and transformations.
Common Mistakes and How to Avoid Them
- Confusing Radians and Degrees: Always ensure you’re using the correct unit when calculating angles.
- Sign Errors: Remember the sign conventions for each quadrant.
- Incorrect Coordinates: Memorize key angle coordinates to avoid mistakes.
FAQs
Q: Why is the unit circle important in trigonometry?
A: It provides a geometric framework for understanding and calculating trigonometric functions.
Q: How do radians relate to degrees?
A: Radians and degrees are two units for measuring angles. 180° equals π radians.
Q: Can the unit circle be used for angles greater than 360°?
A: Yes, by considering the periodic nature of trigonometric functions, angles beyond 360° can be analyzed using the unit circle.
Conclusion
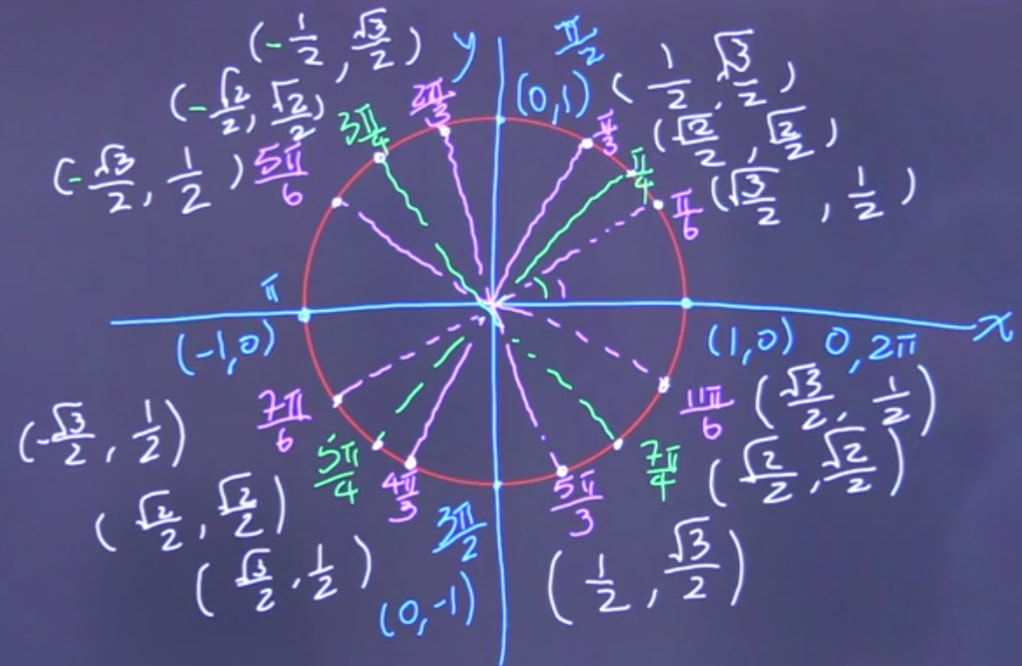
The unit circle chart isn’t just a diagram—it’s a gateway to understanding the very heart of trigonometry, circular motion, and periodic behavior in real-world systems. Whether you’re a high school student, a university math major, a physics enthusiast, or a software developer working in graphics or engineering, mastering the unit circle is non-negotiable.
With its foundation in geometry and algebra, the unit circle links abstract math to practical applications: from calculating angles in architecture to simulating planetary motion in astronomy, or animating rotations in game design.






